Pushing and bouncing air
Some reflections on the Theory and Practice of Pipe Organ
Wind Supply
by Johan Liljencrants
The good old topic of organ air supply surfaced again in the MMD
Pipes Forum in 1999. At that time I learnt a lot from our experienced community
about what devices you employ to get a stable air supply. Here is a brief
review of these components and some of their properties described in acoustical
engineering terms. Special attention is with the problem of regulation
of transient loads, how to keep pressure constant across sudden
changes
in air demand. It is no cookbook on how to make a complete supply system
- a prominent reason is the difficulty to specify what is required - but
hopefully you may find some dimensioning guidelines from examples given.
Basic formulas and diagrams are in SI units [6], but
translations into traditional units are mostly shown in parallel.
In an organ pipe the tone onset is very important and characteristic
and there are several factors to determine this onset. One is the pipe
itself as set up by the voicer. To keep a predictable pipe tone you must
also have control of how rapidly the playing valve opens and how well the
wind supply stands up to the increase in air demand when the pipe goes
on. Also any subsequent pressure changes will modulate the pipe tone, notably
when it sounds while other pipes go on or off, in particular in wide chords.
1. Sources
2. Reservoirs
3. Transmission trunks
4. Compensators
5. Bellows speed
6. Regulators
7. Complete feeder systems
8. References
9. Unit conversions and Air properties
1. Sources
Classical supply to bigger (church) organs up to the decades around 1900
was big weight loaded bellows. Each bellows had a lever to lift it and
the organ blower(s) walked on these levers fast enough to maintain at least
one of the bellows to be active. The regulation aspect here is that air
pressure is then defined by those loading weights, not by the weight of
the organ blower or how fast he works. This kind of source really does
not belong in this section, but to the next of Reservoirs.
Small as well as big street organs are usually powered from bellows,
agitated from a hand operated crankshaft. Modern modifications of these
most often include accumulator driven electric motors or gas engines to
drive them over a belt. Here are the outlines of a classical street organ
feeder [8]:
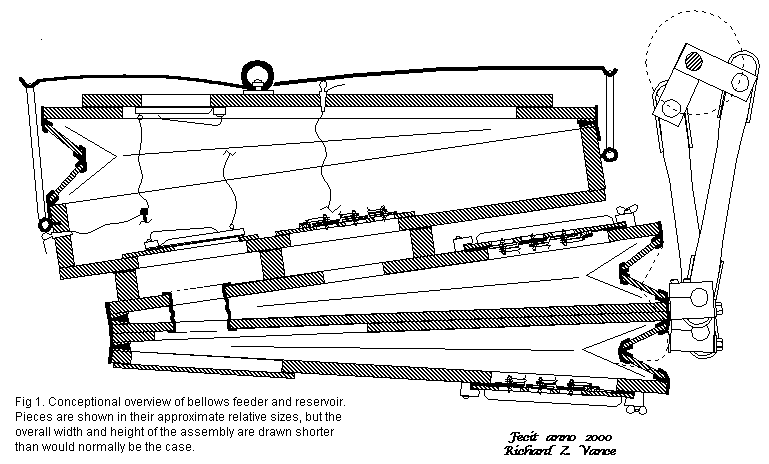
The bottom two wedges constitute a double acting feeder with valves
for the air into the top, spring loaded reservoir. (The second crank connecting
rod drives one more such feeder, hidden in the drawing). Cranking at constant
speed the feeders basically deliver constant airflow, no matter how much
you need and at what pressure. The first regulation here comes with the
feeder output valves, they are joined with adjustable strings to the reservoir
lid. When the reservoir is full they are held open such that the surplus
air returns back into the feeders. This is a very essential feature: when
air consumption is low, then the mechanical power to drive the feeder is
also reduced - the different feeder bellows then exchange the same air
between them and you only have to supply power to overcome friction. Note
removable panels and valves for easy maintenance and a string operated
safety pallet at top of the reservoir.
Without this tying up the feeder valves, the feeder would blow up the
reservoir, were it not for the safety pallet. This one actually implements
another principle of regulation, it is a spill regulator. Any surplus
air is blown off, but in the same time you lose the energy you spent to
pressurize it. Using spill regulation alone you have to provide full power
to the crankshaft all the time. Apart from being wasteful this also makes
noise, so spill regulation is mostly used for very small systems where
simplicity and low cost may be important.
 Fancy
drive alternatives from over the times are now displaced by ubiquitous
electric centrifugal fans. These have radically different properties from
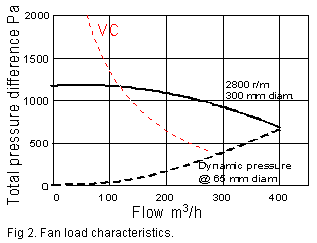
a bellows, you can show them with a load characteristic graph. Fig.
2 is an example of such, how the output pressure can vary as function of
the flow delivered. The red dashed curve, where VC stands for a typical
vacuum cleaner fan, shows a very high pressure at low flow, dropping considerably
as load increases. This common fan type is about the least suitable there
is for an organ. But fans may be radically different from each other. By
proper engineering, including swept rotor blades, you can get a much superior
characteristic having almost constant pressure, as exemplified with the
black solid curve. The figures nearby show typical rotational speed (for
a 3 phase, 50 Hz motor) and diameter for a fan that can deliver pressures
in the 1 kPa (4 inWC) range. A fixed fan design delivers pressure in proportion
to radius and to the square of speed. For higher pressures you would normally
select a bigger fan (or possibly more than one in cascade) rather than
belt drive to a faster and noisier one.
Fancy
drive alternatives from over the times are now displaced by ubiquitous
electric centrifugal fans. These have radically different properties from
a bellows, you can show them with a load characteristic graph. Fig.
2 is an example of such, how the output pressure can vary as function of
the flow delivered. The red dashed curve, where VC stands for a typical
vacuum cleaner fan, shows a very high pressure at low flow, dropping considerably
as load increases. This common fan type is about the least suitable there
is for an organ. But fans may be radically different from each other. By
proper engineering, including swept rotor blades, you can get a much superior
characteristic having almost constant pressure, as exemplified with the
black solid curve. The figures nearby show typical rotational speed (for
a 3 phase, 50 Hz motor) and diameter for a fan that can deliver pressures
in the 1 kPa (4 inWC) range. A fixed fan design delivers pressure in proportion
to radius and to the square of speed. For higher pressures you would normally
select a bigger fan (or possibly more than one in cascade) rather than
belt drive to a faster and noisier one.
There are a few makers of specialized organ fans [5].
Beyond their load characteristic these are distinguished by silent operation
due to careful balancing, solid housings, often cast, and a preference
for sleeve bearings rather than ball bearings. Such fans have a noise level
about 50 to 60 dBA and cost typically three times more than equivalent
industrial fans which are 20 to 30 dB more noisy.
The pneumatic power you supply to an organ is pressure times flow, W=PU.
It is convenient to use SI units for P and U such that the
power comes out in Watts without conversion factors. For instance, in the
fan diagram P=1.1 kPa and U=200 m3/h=0.056 m3/s
gives W=1100*0.056=61 Watts. Installed drive motor nominal power
is normally several times bigger than this pneumatic power. And finally
delivered sound power to the order of 1% of it.
2. Reservoirs
The reservoir obviously holds a spare quantity of pressurized air ready
for immediate use, possibly to fill transient loads bigger than what is
continuously available from the source. A main function however is to
define
a system pressure, which will be F=(total normal force on the
reservoir lid) divided by A=(area of lid). Pressure P=F/A.
Often the reservoir lid is also a sensing element in a regulating system.
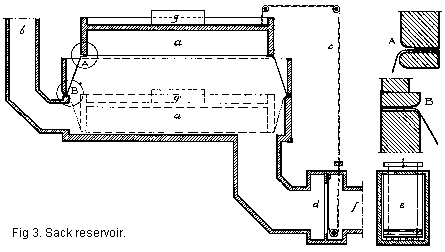 The
reservoir is conventionally a single wedge bellows or a double parallel
moving bellows (church organs). Another variant is the sack reservoir where
the lid is joined to the support frame with a rubber cloth collar that
rolls inside and out as the lid moves, fig. 3 [7]. This
picture also shows a 'curtain regulator' that shuts off the supply coming
in from lower right by way of a chain to the reservoir lid.
The
reservoir is conventionally a single wedge bellows or a double parallel
moving bellows (church organs). Another variant is the sack reservoir where
the lid is joined to the support frame with a rubber cloth collar that
rolls inside and out as the lid moves, fig. 3 [7]. This
picture also shows a 'curtain regulator' that shuts off the supply coming
in from lower right by way of a chain to the reservoir lid.
The lid force may in stationary cases be exerted by weights (iron bars,
stones, concrete blocks), now more often by springs, always so in portable
applications. An easy way to estimate it is to start from the required
pressure, expressed in terms of water column height. Multiply this height
by the lid area - then you get a volume of water having the required weight.
Example 1:
| Pressure 2.5 kPa = 0.25 meters water column, lid area 0.6*0.6=0.36
m2. Water volume would be 0.25*0.36=0.09 m3,
weighing about 90 kg. Lid force has to be 90 kp, about 900 Newtons. 900/0.36=2500
Pa. |
| Pressure 10 inch WC, lid area 2*2=4 sq. ft. Water volume would be (10/12)*4=3.33
cubic ft, at 62.4 lb./cubic ft weighing about 208 lb. Lid force has to
be 208 lb, about the same 900 Newtons. |
The obvious part of the lid force is that from the weight or spring.
A weight will give a constant force while a spring generally delivers a
greater force the more the reservoir is filled. But there is also another
force acting on the lid, namely from the bellows folds. With a sack reservoir
this is essentially small and independent of lid position. But with a gusseted
ribs reservoir this force will vary depending on filling degree.
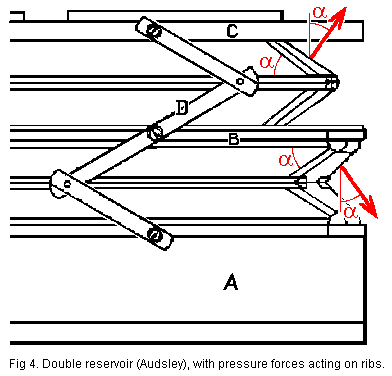 Fig.
4
[1] shows one corner of a double reservoir where I
have inserted red arrows to show the forces from internal pressure acting
on the folding ribs. The magnitude of these forces is pressure times rib
area. They can further be split up into vertical and horizontal components.
These will vary in size, depending on the filling state, indirectly defined
by the rib angle
a.
Fig.
4
[1] shows one corner of a double reservoir where I
have inserted red arrows to show the forces from internal pressure acting
on the folding ribs. The magnitude of these forces is pressure times rib
area. They can further be split up into vertical and horizontal components.
These will vary in size, depending on the filling state, indirectly defined
by the rib angle
a.
The lower bellows is inward folded, between frames A and B, and here
the vertical component on the ribs try to pull the frames together, they
counteract
the pressure on the lid which balances the weight or spring. This effect
is most pronounced when the bellows are almost collapsed since the vertical
component decreases with growing a as
the lid lifts. The horizontal component works the opposite way, it grows
with a, and it makes the ribs try to
wedge the frames apart, it
cooperates with the pressure on the lid.
The total result is that when you fill a single, weight loaded inward
folded reservoir the pressure
decreases as you fill it.
Contrarily, in the upper outward folded bellows between frames B and
C, the rib forces change sign. So when you fill a single, weight loaded
outward
folded reservoir the pressure increases as you fill it. The specific
feature of the illustrated double bellows design is to have these opposing
actions to neutralize each other. But to make this work you must force
frame B to be mid-way between A and C, effected by the pantograph mechanism
D. This double bellows then keeps constant pressure, independent of filling
degree, when compressed by a weight.
 If
you make a square 'camera folded' bellows as in fig. 5 - cylindrical cloth,
two folds out, two in - this is also essentially neutral to the rib forces.
If
you make a square 'camera folded' bellows as in fig. 5 - cylindrical cloth,
two folds out, two in - this is also essentially neutral to the rib forces.
Accounting for those extra forces from the folding ribs, the relation
between the external bellows compression force F and pressure P
can be formulated as a bellows equation:
F/P = A ± B*0.5*(sin(a)*tan(a)-cos(a))
[m2]
where A is the lid area, B is folding rib area (one layer
only, as seen in a top projection drawing of the bellows), and a
is the opening angle of the folds. Plus sign for inward folds, minus for
outward. An important special case is at a=45
degrees, ribs at right angles to each other. Then the complicated coefficient
for B becomes zero and pressure equals the nominal P=F/A.
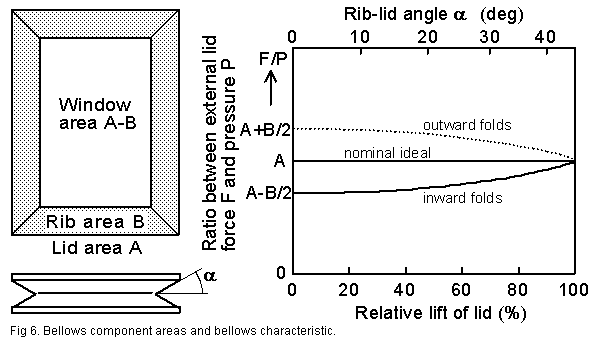
A reservoir is normally supplied from some power machinery and the
forces involved are considerable. With an inward folded bellows there is
a hazard inherent from the rise in the F/P characteristic
shown in fig. 6. Keeping constant pressure, as angle grows you need
a progressively greater force to balance it, indeed infinite force at a=90
deg. It is essential that you limit the angle to protect the bellows
from such overload, otherwise it will be blown out and ripped apart. Usually
you do that with a pallet safety valve on the lid, operated with a string
or a finger toward some fixed structure, as exemplified in fig.
1. Normally you would allow a lid to rib angle
a
no more than about 45 degrees.
With a spring loaded reservoir the spring force increases in proportion
to the lid lift. Then the best is to use an inward folded reservoir. Ideally,
for constant pressure, the force should then grow with a
the same way as the complicated right hand expression. But we can reasonably
well match this with a straight line. For given areas A and B,
and pressure P, we may use for a rule of thumb that the spring force
at full lift should be F(100%) = P*A, and with
the bellows collapsed, F(0%) = P*(A - 0.6*B).
That magic coefficient 0.6 is derived from the criterion that pressure
around 20% lift should be the same as at 100%. Deviation from the ideal
increases with B/A. Using B/A=0.5 as drawn
in fig. 6, then pressure will be some 6% too high around 60% lift. For
better precision you may reduce B, but that implies that the bellows
volume capacity goes down in proportion.
Example 2:
| In example 1 above, where A = 0.36 m2,
P
=
2500 Pa, we already found F(100%) = 900 N, about 90 kp.
Now we also prescribe that 100 % lift is to be 0.1 m. This settles the
rib width to 0.1/sqrt(2) = 0.0707 m. The free window area inside the ribs
is then A-B = (0.6-2*0.0707)2 = 0.21 such that
B
=
0.36-0.21 = 0.15 m2. The rule of thumb renders F(0%)
= 2500*(0.36-0.6*0.15) = 675 N, about 68 kp. This may be reformulated into
a required spring constant to be K = (900-675)/0.1 = 2250 N/m, or
230 kp/m, or 0.23 kp/mm. At full lift the spring(s) should be elongated
from rest length a distance F/K = 900/2250 = 0.4 m, going
down to 0.3 m when bellows is collapsed. |
| In example 1 above A = 22 ft2
=
242 in2
= 576 in2, P = 10 inWC.
For dimensional consistency we convert that into P = 0.361 PSI.
This in an alternative way renders, as we already found, that F(100%)
= A*P = 576*0.361 = 208 lb. Now we also prescribe that 100 % lift
is to be 4 inches. This settles the rib width to 4/sqrt(2) = 2.83 in. The
free window area inside the ribs is then A-B = (24-2*2.83)2
=
336 such that B = 576-336 = 240 in2. The rule of thumb
renders F(0%) = 0.361*(576-0.6*240) = 156 lb. This may
be reformulated into a required spring constant to be K = (208-156)/4
= 13 lb/in. At full lift the spring(s) should be elongated from rest length
a distance F/K = 208/13 = 16 in, going down to 12 in when
bellows is collapsed. |
3. Transmission trunks
The air distribution trunks are a necessary evil and should obviously be
kept as short, as wide, as straight, and as airtight as possible. Their
consequences and countermeasures to those are the main topic of this article.
The trunks are classically built from wood planks or boards. Nowadays metal
or plastic tubing is often more convenient, e.g. tubes and joints with
rubber gaskets as fabricated for sewage plumbing.
3.1. Pressure losses in steady air transport
When you steadily transport a volume flow U using a duct (the general
technical term for a trunk) of length L and diameter D, then
you will suffer a pressure drop P. This drop has two basic components,
the viscous Pvisc and the kinetic Pkin.
Pvisc is the result from the internal viscosity of
air. This is the component generally talked about and it behaves well in
the sense that is is directly proportional to the length of the trunk.
The drop is larger as flow rate increases or the trunk is narrower. Computation
is rather complicated as the flow in most cases is turbulent. The outcome
is however well established from theory and practice combined, and fig.
7 is a diagram tailored to flow and pressure ranges typical with organ
blowing. Data and format of it is taken from a diagram for ventilation
engineers in a standard handbook [4].
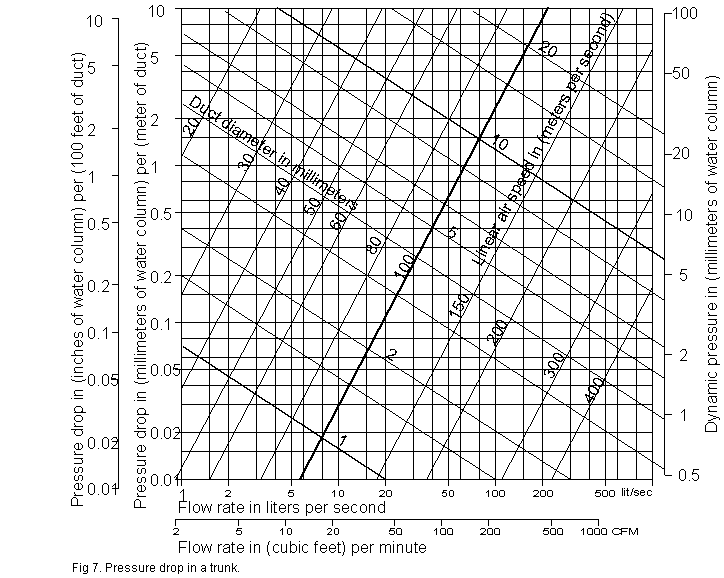
The viscous pressure drop per unit length in a cylindrical trunk for
air at about atmospheric pressure and room temperature.
Step 1: Locate on a bottom horizontal scale the flow rate you
are going to transport.
Step 2: From this point move vertically until you intersect the (right
upward sloping) line for the diameter of your trunk. Mark this intersection
point.
Step 3: Go horizontally to a left scale and find the pressure drop
per unit length.
Step 4: Multiply with the length of your trunk to obtain the total
pressure drop due to viscous friction.
Step 5: At the intersection point of step 2, find from the right downward
sloping lines what is the linear speed of the air inside the trunk.
Step 6: Follow the direction of these downward sloping lines to the
right scale and read the corresponding dynamic pressure. |
Pkin is the sum of additional pressure drops that
come about when you change the shape of the trunk, which implies that the
air is accelerated some way. For instance at the trunk inlet air has to
be accelerated from essentially standstill to a speed V=U/A where
A
is the trunk area. The pressure required to do this acceleration is close
to what is often called the dynamic pressure
Pdyn = 0.5*r*V2
[Pa=N/m2]
The Bernoulli equation for dynamic pressure
Also other area changes like in valves, or any bends in the trunk, will
add to Pkin. In handbooks and catalogs these contributions
are often said to be a certain fraction K of the dynamic pressure,
for instance K=0.3 for a 90 degree large radius bend. Another classical
rule of thumb says that for a sharp elbow the pressure drop is the same
as for 32 diameters length of tube. In other words, when you lay out the
proposed trunk, count the elbows, and add 32 times the diameter of the
proposed trunk diameter for every elbow, to the total length.
Example 3:
Air is conducted from a reservoir holding a pressure of 2.5 kPa, (25
cmWC, 10 inWC) to a chest, using a 50 mm (2 in) diameter tube of total
length 5 m (16.4 ft). The tube has two 90 degree elbows. The flow rate
is 10 liters/second (21 CFM). How much lower is the chest pressure
than that of the reservoir?
The diagram tells the viscous loss to be 1 mmWC/m, totally 5 mmWC for
the 5 meter length. The air speed is 5 m/s and the dynamic pressure 1.5
mmWC, being lost when air accelerates into the tube. With two slow bends
you might lose additionally 2*0.3*1.5=0.9 mmWC. The elbow thumb rule says
2*32 diameters is 3.2 meters, hence drop 3.2 mmWC, considerably more. Total
pressure drop is thus estimated into 8-10 mmWC. Also you would regain some
of the dynamic pressure should the air speed slow down entering the chest
volume. The drop is to the order of 4% of the reservoir pressure. This
is measurable with a water manometer and you might believe this is an acceptable
loss, that you could allow such a long, narrow trunk. |
It is important to note that these pressure drops are for the maximum
desired flow rate chosen for the calculation. Pressure loss is proportional
to the square of the flow, so at lower flows, the loss will be much lower.
In any typical organ, the airflow for any chord in the top octave (1/2')
will consume only about 4.5% of the wind required for a similar chord played
in the bottom (8') octave. At the lower flow of the treble
chord, the pressure drop will be essentially zero. So the calculated loss
will be equivalent to the expected range of deviation in the chest pressure,
depending on the character of the music being played.
Luckily, the effect of increasing the trunk size just a little has an
equally dramatic effect in the opposite direction. For example, going
from a 3" trunk to a 4" trunk cuts the loss in half. The practical
range of available pipe sizes (in America, 1/2", 3/4", 1", 1-1/2", 2",
3" 4", 6", 8", 12", 16") is designed to do approximately that. So
if the calculated range of chest pressure variations seems a little high,
upping the trunk one size will cure that.
The fan load characteristic above also shows a curve
for dynamic pressure. This is found with the Pdyn formula
and the linear air speed V as computed from the flow and the fan
outlet diameter. When the fan is run free, without anything connected to
it (giving 400 m3/h with that specific example fan), then there
will be zero static (over)pressure at both ports. Then all work done by
the fan is used to develop a dynamic pressure, manifest only in the speed
of the output air.
3.2. Pressure losses with dynamic load changes
From such examples you might dimension a distribution system. You might
also check it and feel satisfied from what you read on a manometer. But
when you actually play the organ, when air demand changes rapidly, then
everything may go wrong with chest pressure - and a slow manometer will
not tell you! There will be big fast transients. Sudden pressure drops
when you turn on a set of pipes, and surges when you turn them off. A constantly
sounding pipe on the same chest will then have a bad supply, most probably
causing it to give an abnormally modulated sound.
To handle this we must leave statics and DC flow aerodynamics and switch
into acoustics. The big issue is that now we are talking about higher frequencies
and transients, not the continuous DC flow of the 'plumber's diagram' above.
Now, looking at a trunk, we can represent it mathematically two different
ways, either as an acoustical mass, or as an acoustical transmission line.
The simpler way is to regard the air inside the trunk as an acoustical
mass, a simple discrete element. This mass has an inertia and it will take
time and pressure exerted on it to make it accelerate. 'Discrete element'
presumes the enclosed air moves as a single unit, all parts of the air
column move in synchrony. Whether this is reasonable or not depends on
what frequency range or what time scale we are interested in. A convenient
way to formulate this is that the trunk must be 'acoustically small', meaning
small compared to wavelength.
The acoustical mass of a tube is simple to derive from Newton's law
in mechanics: Force=mass*acceleration. In acoustical terms the same will
read: Pressure=(acoust. mass)*(time derivative of flow). From this you
can eventually derive
Mtube = r L/A
[Ns2/m5 = kg/m4]
Acoustical mass of a tube
where L is the length and A is the area of the tube, r
is
density of air.
Example 4:
| With the 5 meter by 5 cm diameter tube Mtube = 1.2*5/(p*0.0252)
= 3056 Ns2/m5. Let us suddenly by means of a valve
put the 2.5 kPa (2500 N/m2, 10 inWC) pressure to the input end
of it. Then flow will accelerate, dU/dt=P/Mtube=2500/3056=0.818
m3/s2. Queer unit? In each second, flow will increase
by 818 liters/second (this will not go on for a very long time, soon flow
will be limited by viscosity as per section 3.1). But it means that for
the flow to reach 10 liters/sec will take some 10/818=12 milliseconds.
But in that time sound will propagate a distance approximately 0.012*c=4.1
m which is less than the tube length. This tells there is something wrong,
flow cannot possibly propagate faster than c. The trunk is too long to
regard as a discrete element on this time scale, however you come somewhere
near a plausible answer when you add the 5 meter propagation time of 15
milliseconds to those 12 milliseconds rise time. |
The more complex and accurate way to treat a trunk should be used when
the dimensions, particularly the length, are not small. Then we could regard
it an acoustical transmission line which can be tackled using two different
key properties, the speed of sound c, and its acoustical
impedance Z.
In a wide trunk c is essentially the same as in free air,
but in a narrow channel (like in the tubes for pneumatic control in organs
or player pianos) it is up to 15% lower because of isothermal conditions
rather than adiabatic.
Acoustical impedance by definition is the ratio between pressure and
flow, Z = P/U. Pressure is measured in Pascals = Newtons/meter2,
flow in meter3/second, so impedance is consequently in Newton*seconds/meter5.
Alas nobody has any intuitive feeling for that unit.
Now hopefully knowing what impedance is, what is its value for a trunk
or tube? Derivation of this is a bit complex, so I just tell you it is
Ztube = rc/A
[Ns/m5 ] Acoustical
impedance of a tube
Air density times speed of sound, divided by tube cross-sectional area
A.
This impedance giving the ratio between P and U now makes
it possible to estimate the pressure at the loaded end when you give it
a sudden, transient load. To do this in detail requires computers and programming,
but using sheer reasoning we can still look at the following:
Horror example 5:
| With our 5 meter by 5 cm diameter tube the impedance in SI units is
Z
= 1.2*343/(p*0.0252) = 2.1*105
Ns/m5. This trunk comes from a remote feeding reservoir with
2500 Pa (25 cmWC, 10 inWC) pressure. Suppose we now suddenly start drawing
U=10
liters/second from the tube. By way of the impedance we can then find how
much the pressure drops at the tube end: P = ZU = 2.1*105
*0.010 = 2100 Pa. Essentially a short circuit, almost none of the original
pressure remains at the receiving end!. What happens next is a wavefront
rushes upstream the tube at the speed of sound, sending backwards the required
flow. The substance of this flow comes from the decompression of the air
in the tube. The wavefront will reach the reservoir after 5/c= 0.015 seconds.
Not until now the reservoir 'knows' what happened at the far end of the
tube and gets its chance to feed the tube with a flow. But the wave that
traveled up the tube hits a low impedance in the reservoir, it is almost
totally reflected back toward the loaded end with opposite pressure polarity
and the reservoir starts feeding with twice the required flow. After
another 15 ms this surge reaches the receiving end, and if we still insist
on extracting 10 l/s then pressure will jump up to the reservoir 2500 Pa
plus the 2100 Pa surge (minus some because of losses), considerably more
than the nominal pressure!
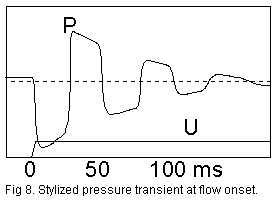 The
surge wave will continue for some time bouncing back and forth in the trunk
which actually behaves just like an organ pipe resonator. This idealized
fig. 8 shows pressure vs. time at the receiving end of the trunk. The
surge wave will continue for some time bouncing back and forth in the trunk
which actually behaves just like an organ pipe resonator. This idealized
fig. 8 shows pressure vs. time at the receiving end of the trunk.
In a practical situation things are even more complex, for instance
the flow drawn will not naturally stay constant when the available pressure
fluctuates this way, rather it will inherit some of the modulation from
the pressure. This very fact together with viscous damping is the reason
the air bouncing dies out in a few periods. The dotted line suggests the
average pressure at the far end. It is a little bit lower than the reservoir
pressure, namely that tiny drop we calculated from the 'plumber's
diagram' in section 3.1, example 3. |
With a shorter trunk of same diameter the variations will be just as
large. The trunk area and the load change alone define the magnitude of
the pressure variations. But with a shorter trunk the oscillations are
faster, less sound propagation time from end to end. So with a short trunk
the transients may be over in just a few tens of milliseconds.
Example 6:
| Same 10 liter/second load change, but we will allow no more than 4%
drop in the 2500 Pa pressure, that is 100 Pa. The impedance will then have
to be at most Z=P/U=100/0.01=10000 Ns/m5,
tube area A=rc/Z=1.2*343/10000=0.041m2,
at least 23 cm (9 in) diameter! |
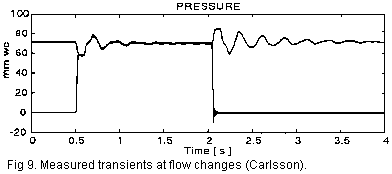 Here
are two illustrating examples taken from the real world. Recently Carlsson
[2]
showed the pressures at the receiving end of the trunk and in the note
channel (on the downstream side of the playing valve), recorded from a
church organ, fig. 9. This trunk is 13.5 m (44.4 ft) long with a square
cross section of 15 cm (6 in) and the transient load change was 8.6 l/s.
The initial transient pressure loss is about 20%. This is believed to be
representative, it exhibits the same behavior as in example
5, but not to such extreme degree. The pressure oscillates at about
4 Hz, somewhat lower than ideally expected for this length of the trunk.
The difference is ascribed to a lowered sound speed and to additional effects
from reservoir (wedge) shape, wall elasticity and adjacent channels.
Here
are two illustrating examples taken from the real world. Recently Carlsson
[2]
showed the pressures at the receiving end of the trunk and in the note
channel (on the downstream side of the playing valve), recorded from a
church organ, fig. 9. This trunk is 13.5 m (44.4 ft) long with a square
cross section of 15 cm (6 in) and the transient load change was 8.6 l/s.
The initial transient pressure loss is about 20%. This is believed to be
representative, it exhibits the same behavior as in example
5, but not to such extreme degree. The pressure oscillates at about
4 Hz, somewhat lower than ideally expected for this length of the trunk.
The difference is ascribed to a lowered sound speed and to additional effects
from reservoir (wedge) shape, wall elasticity and adjacent channels.
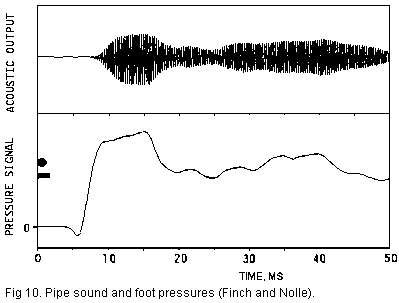
Similarly the wind chest itself contributes variations due to internal
waves in its channels that are generated downstream when a note valve opens.
Fig. 10 is an example, adapted from Finch and Nolle [3].
At bottom it shows note channel pressure near the foot of the pipe after
the note valve has begun opening at time 0. At top the tone from the pipe,
clearly modulated by the pressure variations. The filled circle marks supply
pressure and the solid bar the somewhat lower pressure entering the note
channel, after the playing valve.
Mementos of this section are: With transient loads the pressure variations
at the end of a trunk may be much bigger than you see with an ordinary
slow manometer. They may severely affect the pipe sound. To study them
you will need a fast pressure transducer. To reduce them you can
use a wider trunk, i.e. having a lower impedance. But to reach a sufficiently
low impedance the trunk area probably would have to be inordinately large.
To efficiently combat the pressure variations due to a varying
load to a trunk you must introduce additional components.
4. Compensators
Every electronics engineer knows that in a power supply you must install
reservoir, or decoupling, capacitors to do away with voltage transients.
This is a direct analogy to our air supply problem. Next thing is then
to introduce the concept of 'acoustical capacitance'. This is defined
as C=DV/DP
where
DV is change in volume and DP
is change in pressure. In SI units V is in [meter3] and
P
in [Pascal=Newton/meter2], so capacitance is in [meter5/Newton],
again pretty hopeless to grasp intuitively.
The prototype for an acoustical capacitance is a closed stiff container
of volume V. When you compress the air inside it by pumping in that
DV,
then pressure will rise the amount
DP.
By use of the gas law you can eventually derive the formula
C = V/(rc2)
[m5/N] Acoustical capacitance of a closed
volume V
Example 7, recalling the horror example
5:
| During the first 30 ms interval the rarefaction wave runs to the reservoir
and then comes back, apparently with fresh air. During that time interval
the 10 liter/second flow means we would consume DV=0.3
liter=0.0003 m3. Suppose we connect a capacitance container
at the receiving end hoping to let this one supply the necessary air while
we are waiting. Also suppose we will accept a pressure drop DP=250
Pa (2.5 cmWC, 1 inWC). The container must then have a capacitance C=DV/DP=0.0003/250
and with the above formula we find its necessary volume to be V=C*rc2=0.0000012*1.2*3432=0.169
m3 (6 ft3). Probably we would not accept such a big
device for the purpose. |
But there is a marvel called a bellows. Ideally a bellows can render
an infinite capacitance, meaning the pressure is constant (DP
=0) when you push in or take out a limited volume DV.
- A concussion bellows is the standard decoupling device used to
subdue pressure variations such as those we discuss here. There are two
common forms, 'winkers' and 'schwimmers'.
A winker is a small hinged bellows, often mounted in the wall of a trunk.
It is pushed on by a compass spring to match the average pressure. You
can fine adjust the point where the spring force is applied to a suitable
distance from the hinge of the moving board.
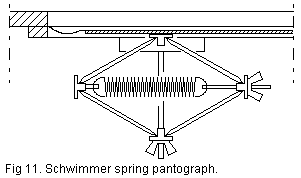 In
a schwimmer the moving wall is a flat bellows cloth supporting a light
panel and this is often mounted in the wall of the pipe chest itself, the
ultimate location to avoid any ducting between compensator and point of
use.
In
a schwimmer the moving wall is a flat bellows cloth supporting a light
panel and this is often mounted in the wall of the pipe chest itself, the
ultimate location to avoid any ducting between compensator and point of
use.
A difficulty with concussion bellows is that you have to match the spring
force quite precisely to the actual pressure. It is a passive device that
adapts to the pressure, whatever this happens to be, it does not regulate
it. If the spring force is too high or too low, then the bellows will stay
in one of its end positions and will not be able to supply any volume displacements.
With a schwimmer adjustable pantograph like in fig.11 you can adjust both
the spring constant and the spring force operating on the plate. You can
then come very close to infinite capacitance, i.e. constant pressure independent
of plate position, but for this to be practical pressure must be closely
regulated.
Many organ chest designs, such as Aeolian, Pitman or WurliTzer, have
the bottom of the chest occupied with various machinery, and there is no
room for a schwimmer. These makers solved the problem differently,
by placing another regulator close-coupled to the chest with a large opening.
This essentially isolated the chest from any dynamic or pressure loss effects
of the trunking. See Section 7 for an analysis of the entire wind
supply configuration, including this feature.
5. Bellows speed
An issue with concussion bellows and regulators is how fast they react.
In 3.2 the theme was about the effort to accelerate a mass of air inside
a trunk. Now, about how difficult to accelerate the lid of a bellows. Again
we can use the property of acoustical mass, and we can find (by way of
how area relates force to pressure and speed to flow) an expression for
the acoustical mass
Ma of a bellows lid as
Ma = Mm/A2
[kg/m4]= [Ns2/m5]
Acoustical mass of a piston
where Mm is the mechanical mass in kg and A is
the lid area in m2.
Intuition is strongly connected to mechanical mass (in kg or lb) -
a heavy mass is hard to accelerate. However this does not directly apply
when we look at the consequences for the air, then we must also account
for the coupling area. The result of this is the acoustical mass - one
may rephrase this into (pressure drop) per (flow increase rate) - admittedly
difficult to understand by intuition, but it tells an important tale.
Examples 8: Table relating mehanical mass and
area to acoustical mass. The first two items represent air in trunks. The
last three represent the lids for a small bellows and a big reservoir.
|
Item
|
Mm [kg]
|
A [m2]
|
Ma [kg/m4]
|
|
Trunk 5 m, 5 cm diameter
|
0.0118
|
0.00196
|
3056
|
|
Trunk 5 m, 10 cm diameter
|
0.0471
|
0.00785
|
765
|
|
Small bellows, 30 cm square, spring loaded
|
1
|
0.09
|
123
|
|
Small bellows, 30 cm square, weight loaded for 2.5 kPa
|
22.5
|
0.09
|
2770
|
|
Richard V:s big weight loaded reservoir
|
400
|
3.6
|
31
|
One might believe that 12 tiny grams of air in the 5 meter, 5 cm dia.
tube should not do too much to slow down the air supply. But the resulting
Ma says it indeed does so quite a lot! It is 25 times more difficult
to accelerate the air in this trunk than it is to accelerate the small
spring loaded bellows lid. So such a small bellows would do a lot of good
as a compensator if you have that trunk. On the other hand, if you want
it to maintain a sizable pressure using a weight instead of a spring, this
weight would slow down the response of the bellows to make it good for
nothing in the present circumstances.
The last example underlines the significance of area. Despite an enormous
amount of iron to accelerate it is very fast responding. Mostly valid:
bigger is better.
6. Regulators
The purpose of a pressure regulator is to keep pressure at its output to
be constant, whatever input pressure you supply and whatever flow load
you demand. Any regulator has two main components: a sensor to monitor
what is the actual output pressure, controlling an effector, some
kind of valve that opens up just enough for the unregulated input. This
can be implemented many ways, but here we limit ourselves to simple mechanical
solutions, applicable to organs.
A regulator may be characterized by its 'droop', telling how much pressure
drops, DP, when you increase flow DU.
The ratio between those two is then measured in [N/m2]/[m3/s]
= [Ns/m5]. This is nothing else but acoustical impedance once
again. Low droop and low (output) impedance is the same thing. Two factors
decide this droop, or impedance. One is the sensor sensitivity. With our
simple mechanically operating regulators the sensor is a spring and bellows.
The spring compliance together with the bellows characteristic tell how
far the bellows lid is displaced by any pressure change DP.
The other factor is how big flow change DU
is
induced by the effecting valve when displaced this much.
Next interesting property is the speed of regulation. This is where
the preceding section 5 about bellows speed comes in,
the acoustical mass (not its mechanical in kg) of the sensor bellows puts
a limit to its reaction speed.
An additional important feature with a regulator is its stability. Theoretically,
the simple regulators considered here are mass-spring systems, so called
first order, which should always be stable. But even within this narrow
scope practical solutions are not always so, there may be additional elastic
and inertial elements introducing extra delays and a more complicted higher
order behavior. In particular the load can make for problems, it may for
instance be another trunk where waves can propagate back and forth like
in example 5 and present a complicated situation for
the regulator. Also the wedging action of bellows ribs may cause a negative
acoustical capacitance (meaning pressure goes down rather than up when
you inject an air volume) which in itself is enough to trigger instability.
Fig. 12 shows four regulator variants a - d. In all cases the unregulated
input enters at the left side, and all have the same sensor element at
the output, namely a bellows at top where the lid area and the spring force
define what the regulated pressure is going to be. An essential feature
for a good regulator, and for all these, is that the input unregulated
pressure does not put any direct force on the sensor, neither any force
to operate the valve - the output pressure should be independent of the
input..
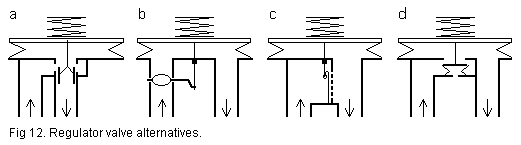
a has a sliding cylinder valve, the principle is the same as
a knife valve regulator, common in player pianos. It may be difficult to
make the slider with enough precision. If there is some play between it
and the outer cylinder to ensure smooth running, then it will not be airtight
enough when there is no load and the output pressure may rise beyond control.
This can be somewhat repaired by making another hole in the output tube,
bleeding it to atmosphere when the plunger goes up above the closed position.
b is a variation using a "stove damper", "butterfly", or rotating
disc as the inlet valve, the usual arrangement on the Spencer Orgoblo blower
system so common on old American organs. In practice, the damper
is weighted closed, and opened by a long chain through pulleys, from the
top of the reservoir to the damper crank on the fan discharge. Crude, but
effective if you accept the low speed caused by the weight.
c with a rolling rubber cloth curtain against a grid is a quite
good workaround to ease leakage problems. The soft curtain will rest tightly
against its supporting grid and its actuating rod is easy to lead through
a leather packing or just a small hole. This item is the same device as
the sack reservoir in section 2. In all cases a-c the regulating valves
have a relatively long mechanical travel between their fully open and closed
positions. This impedes regulation accuracy but improves stability.
d is a classical design, inspired from the Aeolian organ with
Zeb Vance. Here the regulating valve is just a disk covering a hole, easy
to make it airtight with a leather gasket. Its very essential distinctive
feature is the small relief bellows below the disk. This one insures
independence from the input pressure with the important proviso that its
bellows cross sectional area must be about the same as the valve hole area.
The valve disk requires a quite small displacement between open and closed
positions. Speed of regulation accords with the acoustical mass of the
lid and there are no critical friction elements. Indeed it may easily become
too fast, meaning unstable. This is very conveniently damped by the viscous
gas friction in the hole connecting the interior of the relief bellows
to the ambient - in case of instability you can slow regulation down using
a smaller hole.
The area of the regulator valve opening should be perhaps twice the
areas of the connecting trunks. Because the flow path is rather irregular
in the valve region a small opening would give an unnecessary kinetic pressure
drop in it when fully open.
All the illustrated regulators are shown with a comparatively big bellows
lid sensing the output regulated pressure. This is very deliberate. First
reason is this enables the lid to exert a considerable force on the valve
to overcome friction and other disturbances, this insures precision. Second,
it automatically serves as a secondary reservoir/compensator.
7. Complete feeder systems
A complete feeder system is more complicated to analyze than the sum of
its components, but some additional aspects can be illustrated with the
scenario of fig. 13 - of course there are other ones possible. Top half
is a schematic drawing of a source, a trunk, a regulator/concussion bellows,
and finally the load in form of a chest. Below that is a circuit diagram
of the same thing, it intentionally looks like an electrical one. This
is the kind of thing you use in acoustics to compute what is happening.
Such is nowadays done with network simulation computer programs, but classically
it was simulated with such electrical analog circuits, using plain
capacitors, inductors, and resistors.
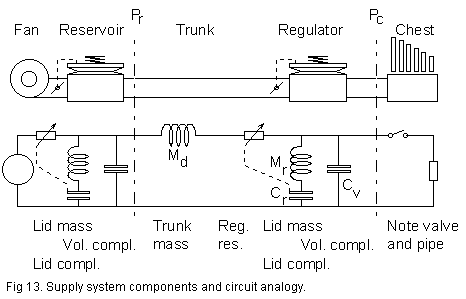 The
left basic supply, a feeder and reservoir, is supposed to deliver a constant
pressure
Pr whatever you load it with. To that end it
is normally a complete regulated system in itself, it has basically the
same elements and works the same way as the following regulation system.
With fan blowers it is common that the first regulating valve (controlled
by the reservoir lid) alternatively is put at the fan intake rather than
at its outlet. Then follows a trunk, the problem child, leading to the
wind chest where pressure is Pc. The trunk causes temporary
pressure drops and surges at changes in the load. To close or open the
switch in the electrical diagram corresponds to start or stop playing pipes.
From the circuit diagram we may describe the middle supply regulator system,
between Pr and Pc, to have three branches,
there are three different ways for flow to arrive at the note valve switch:
The
left basic supply, a feeder and reservoir, is supposed to deliver a constant
pressure
Pr whatever you load it with. To that end it
is normally a complete regulated system in itself, it has basically the
same elements and works the same way as the following regulation system.
With fan blowers it is common that the first regulating valve (controlled
by the reservoir lid) alternatively is put at the fan intake rather than
at its outlet. Then follows a trunk, the problem child, leading to the
wind chest where pressure is Pc. The trunk causes temporary
pressure drops and surges at changes in the load. To close or open the
switch in the electrical diagram corresponds to start or stop playing pipes.
From the circuit diagram we may describe the middle supply regulator system,
between Pr and Pc, to have three branches,
there are three different ways for flow to arrive at the note valve switch:
#1. A 'distant' branch comprising the trunk, slowly reacting because
of the inertia of the enclosed air mass. From the definition of acoustical
mass we can estimate a characteristic time constant like in example
4 Dt=(Md*DU)/(Pr-Pc).
A high acoustical mass Md for the trunk and a large flow
increase
DU
will make it takes a long
time Dt before supply stabilizes. You
can shorten that time by widening the trunk (decreasing
Md)
or increasing the regulator margin
Pr-Pc,
the pressure difference between reservoir and chest.
#2. A 'near' branch where the movement of the regulator bellows lid
compliance Cr delivers the temporarily required extra
puffs of air at transient loads, until the 'heavy' air in the trunk has
had its time to accelerate. Its speed to do this is limited by the acoustical
mass Mr of the lid, examples 8. To
be efficient the lid acoustical mass must be appreciably smaller
than that of the trunk. To be
sufficient the lid area and displacement
must be big enough to supply the flow during the transient time Dt.
This
can be translated into a rough estimate for necessary bellows displacement
volume to be Vb=DU*Dt.
#3. A 'fast' branch with the acoustic capacitance Cv
of the local regulator bellows volume and other nearby volumes. This one
delivers air immediately by virtue of its decompression, essentially without
inertia, but has little capacity (!). V/(r*c2)
is small with reasonable volumes, this amount of air is enough only for
very short times. It is conventional good practice to have a large volume
here, but this will hardly be sufficient anyway, recall
example
7.
When you stop the loading airflow, then the trunk flow carries on by
its inertia and rapidly fills up the regulator bellows such that its valve
closes abruptly. The trunk flow then suddenly 'hits the wall' and there
will be an appreciable pressure surge at the regulator input which can
be computed from Ztube and U, compare horror example
5. This underlines it is necessary the regulator valve be insensitive
to input pressure, otherwise it might not be capable of preventing this
surge to proceed into the regulated chest area.
8. References
[1] From Audsley, G A: The Art of Organ-Building, (1905),
Dover 1965, vol II, p 690, fig. CCCLXXVII
[2] Carlsson, T.: On wind system dynamics of pipe
organs. Lic. thesis, Chalmers Univ. of Technology, Göteborg 1999,
fig. 18.
[3] Finch, T. L., Nolle, A. W.: Pressure wave reflections
in an organ note channel. J. Acoust. Soc. Am. 79(5), May 1986, pp 1584-1591.
[4] Karlebo handbok. A different source is http://www.process-support.com/html/pressure_drop.html
where you can enter arbitrary data and have the drop computed by a Java
applet, provided you give the necessary parameters in SI units. These two
sources render essentially the same results.
[5] See e.g. http://www.laukhuff.de/english/ventus_e.html
[6] See http://www.physics.nist.gov/Pubs/SP811/contents.html
for a survey of SI units
[7] Supplied by courtesy of Hans van Oost
[8] By courtesy of Richard Z Vance
9. Unit conversions and Air properties
Unit conversions
| Quantity |
From traditional units to SI |
From SI to traditional units |
Note |
| Length |
1 in = 0.0254 m
1 ft = 0.3048 m |
1 m = 39.37 in
1 m = 3.281 ft |
|
| Area |
1 in2 = 6.4516 cm2
1 ft2 = 0.0929 m2 |
1 m2 = 1550 in2
1 m2 = 10.764 ft2 |
|
| Volume |
1 in3 = 16.387 cm3
1 ft3 = 28.317 l |
1 l = 61.023 in3
1 m3 = 35.31 ft3 |
|
| Flow |
1 m3/min = 16.67 l/s
1 m3/h = 0.2778 l/s
1 CFM = 0.472 l/s |
1 l/s = 0.06 m3/min
1 l/s = 3.600 m3/h
1 l/s = 2.119 CFM |
.
.
cubic ft per min |
Mass
(Weight) |
1 oz = 28.35 g
1 lb = 0.4536 kg |
1 kg = 35.27 oz
1 kg = 2.205 lb |
|
| Force |
1 kp = 9.810 N
1 lb = 4.450 N |
1 N = 0.102 kp
1 N = 0.225 lb |
|
| Pressure |
1 cmWC = 98.1 Pa
1 inWC = 249 Pa
1 PSI = 6.897 kPa |
1 kPa = 10.2 cmWC
1 kPa = 4.01 inWC
1 kPa = 0.145 PSI |
cm of water column
inches of water column
pounds per sq inch |
Air properties at atmospheric pressure and 20 deg C:
|
Quantity
|
Symbol
|
Value in SI units
|
Value in Traditional units
|
|
Density
|
r
|
1.2 kg/m3
|
0.075 lb/ft3
|
|
Speed of sound
|
c
|
343 m/s
|
1125 ft/s
|
10. Acknowledgement
Richard Z. Vance gave many valuable suggestions, improvements, and contributions
in the process of reviewing this manuscript.
Johan Liljencrants 2001-12-18

 Fancy
drive alternatives from over the times are now displaced by ubiquitous
electric centrifugal fans. These have radically different properties from
a bellows, you can show them with a load characteristic graph. Fig.
2 is an example of such, how the output pressure can vary as function of
the flow delivered. The red dashed curve, where VC stands for a typical
vacuum cleaner fan, shows a very high pressure at low flow, dropping considerably
as load increases. This common fan type is about the least suitable there
is for an organ. But fans may be radically different from each other. By
proper engineering, including swept rotor blades, you can get a much superior
characteristic having almost constant pressure, as exemplified with the
black solid curve. The figures nearby show typical rotational speed (for
a 3 phase, 50 Hz motor) and diameter for a fan that can deliver pressures
in the 1 kPa (4 inWC) range. A fixed fan design delivers pressure in proportion
to radius and to the square of speed. For higher pressures you would normally
select a bigger fan (or possibly more than one in cascade) rather than
belt drive to a faster and noisier one.
Fancy
drive alternatives from over the times are now displaced by ubiquitous
electric centrifugal fans. These have radically different properties from
a bellows, you can show them with a load characteristic graph. Fig.
2 is an example of such, how the output pressure can vary as function of
the flow delivered. The red dashed curve, where VC stands for a typical
vacuum cleaner fan, shows a very high pressure at low flow, dropping considerably
as load increases. This common fan type is about the least suitable there
is for an organ. But fans may be radically different from each other. By
proper engineering, including swept rotor blades, you can get a much superior
characteristic having almost constant pressure, as exemplified with the
black solid curve. The figures nearby show typical rotational speed (for
a 3 phase, 50 Hz motor) and diameter for a fan that can deliver pressures
in the 1 kPa (4 inWC) range. A fixed fan design delivers pressure in proportion
to radius and to the square of speed. For higher pressures you would normally
select a bigger fan (or possibly more than one in cascade) rather than
belt drive to a faster and noisier one.
 The
reservoir is conventionally a single wedge bellows or a double parallel
moving bellows (church organs). Another variant is the sack reservoir where
the lid is joined to the support frame with a rubber cloth collar that
rolls inside and out as the lid moves, fig. 3
The
reservoir is conventionally a single wedge bellows or a double parallel
moving bellows (church organs). Another variant is the sack reservoir where
the lid is joined to the support frame with a rubber cloth collar that
rolls inside and out as the lid moves, fig. 3  Fig.
4
Fig.
4
 If
you make a square 'camera folded' bellows as in fig. 5 - cylindrical cloth,
two folds out, two in - this is also essentially neutral to the rib forces.
If
you make a square 'camera folded' bellows as in fig. 5 - cylindrical cloth,
two folds out, two in - this is also essentially neutral to the rib forces.


 The
surge wave will continue for some time bouncing back and forth in the trunk
which actually behaves just like an organ pipe resonator. This idealized
fig. 8 shows pressure vs. time at the receiving end of the trunk.
The
surge wave will continue for some time bouncing back and forth in the trunk
which actually behaves just like an organ pipe resonator. This idealized
fig. 8 shows pressure vs. time at the receiving end of the trunk.
 Here
are two illustrating examples taken from the real world. Recently Carlsson
Here
are two illustrating examples taken from the real world. Recently Carlsson

 In
a schwimmer the moving wall is a flat bellows cloth supporting a light
panel and this is often mounted in the wall of the pipe chest itself, the
ultimate location to avoid any ducting between compensator and point of
use.
In
a schwimmer the moving wall is a flat bellows cloth supporting a light
panel and this is often mounted in the wall of the pipe chest itself, the
ultimate location to avoid any ducting between compensator and point of
use.

 The
left basic supply, a feeder and reservoir, is supposed to deliver a constant
pressure
Pr whatever you load it with. To that end it
is normally a complete regulated system in itself, it has basically the
same elements and works the same way as the following regulation system.
With fan blowers it is common that the first regulating valve (controlled
by the reservoir lid) alternatively is put at the fan intake rather than
at its outlet. Then follows a trunk, the problem child, leading to the
wind chest where pressure is Pc. The trunk causes temporary
pressure drops and surges at changes in the load. To close or open the
switch in the electrical diagram corresponds to start or stop playing pipes.
From the circuit diagram we may describe the middle supply regulator system,
between Pr and Pc, to have three branches,
there are three different ways for flow to arrive at the note valve switch:
The
left basic supply, a feeder and reservoir, is supposed to deliver a constant
pressure
Pr whatever you load it with. To that end it
is normally a complete regulated system in itself, it has basically the
same elements and works the same way as the following regulation system.
With fan blowers it is common that the first regulating valve (controlled
by the reservoir lid) alternatively is put at the fan intake rather than
at its outlet. Then follows a trunk, the problem child, leading to the
wind chest where pressure is Pc. The trunk causes temporary
pressure drops and surges at changes in the load. To close or open the
switch in the electrical diagram corresponds to start or stop playing pipes.
From the circuit diagram we may describe the middle supply regulator system,
between Pr and Pc, to have three branches,
there are three different ways for flow to arrive at the note valve switch: