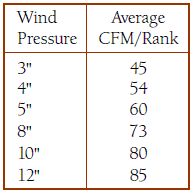
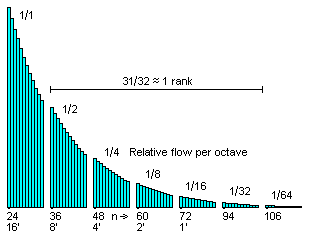
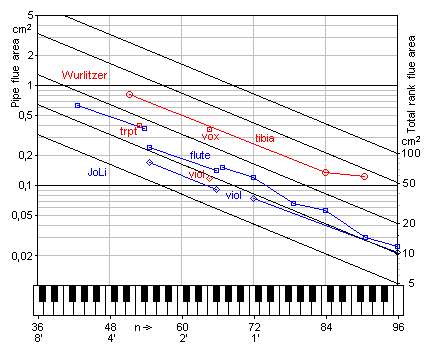
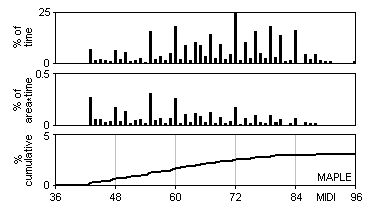
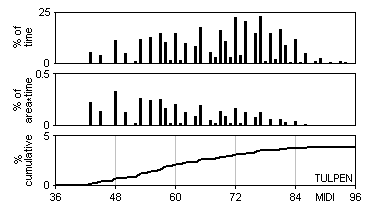
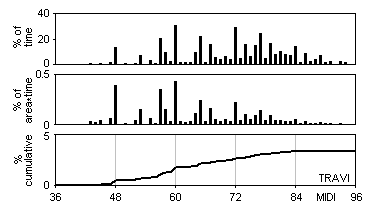
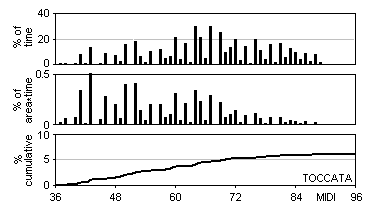
Function and pressure in a centrifugal fan
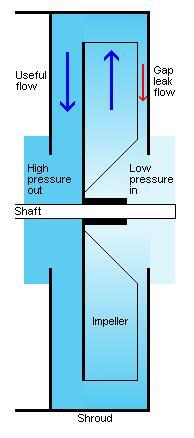
Axial (propeller, turbine) fans produce much flow, but also noise, and typically give nowhere near enough pressure for an organ. We dismiss this fan type from the discussion and concentrate on the centrifugal fan in which a housing encloses a rotating impeller with vanes. The housing has an air intake near the hub of the impeller and an output port near its periphery.
These vanes make the air follow the impeller rotation such that air is pressed toward the periphery by centrifugal force. Based on the basic centrifugal force formula G = m ω2 r (force G, mass m, angular speed ω, radius r) you can set up an integral for the pressure buildup from impeller hub out to perihery. Omitting tedious computational detail the integrated result comes out as a pressure Pc = ρ s2 / 2 (air density ρ, impeller periphery speed s). Now, additional to this pressure rise, the air in the housing outside the impeller also has received a tangential speed of the same magnitude s. If you block the fan output such that there is no airflow, this stagnation invokes an additional pressure rise of about the same magnitude Pc, but this time because of the Bernoulli relation between speed and dynamic pressure, see below.
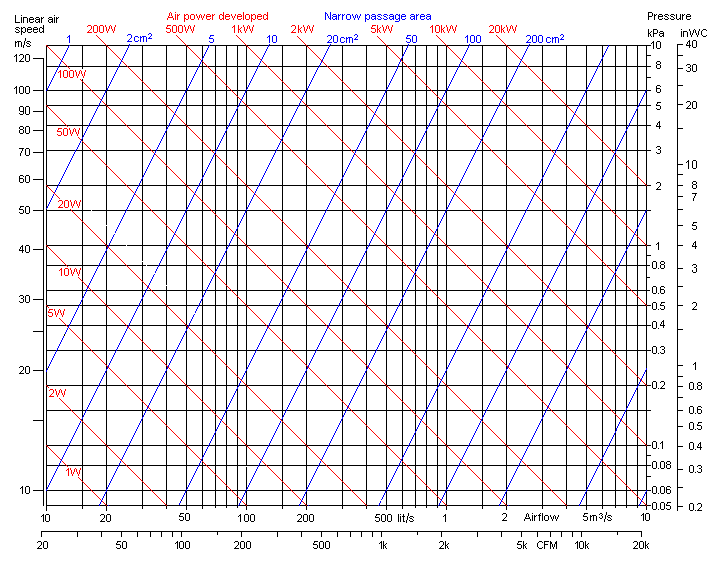
The approximate rule-of-thumb result is that the pressure produced at zero flow is 2Pc = ρ s2. This very simple formula is shown in Fig 1 where s is derived from impeller diameter and rotational speed.
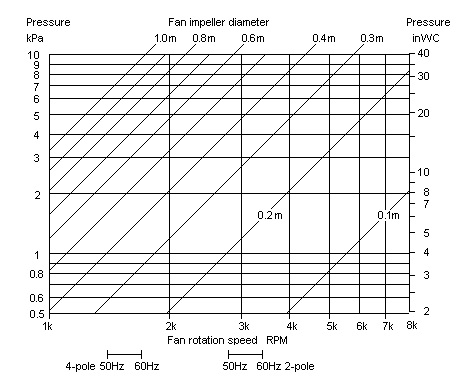
Fig1. The vertical scale is for the benchmark static pressure obtainable from a single centrifugal fan, given rotation speed and impeller diameter.
| Pressure is
proportional to impeller diameter squared Pressure is proportional to impeller RPM squared |
This is the stagnation pressure you can expect from a centrifugal fan, the pressure when output is blocked and no flow is taken out. A first point is that this pressure is linked to the diameter of the impeller and its rotation speed. Engineering inventions like shaping the rotor blades can change it to some degree from the indicated value, but not very radically. Textbook knowledge says that forward swept blades increase pressure, backward swept lower it when flow increases in the low flow region.
If you limit diameter (to keep space down) and speed (to keep noise down) the only remaining option to elevate pressure is to put two or more fans in cascade, one driving the next. Unless you use a belt drive, with common AC motors there are normally only two options for the speed, either 'low' 1400/1700 or 'high' 2800/3400 RPM, depending on motor design and whether you have 50/60 Hz mains.
Dynamic pressure
Because of its formal likeness we may at this point recall the concept of dynamic pressure. This is one of the terms of Bernoulli's equation, which is essentially an equation of energy conservation for a fluid in motion. The dynamic pressure is equal to the difference between the stagnation pressure and the static pressure. Static pressure can be identified for every point in a body of fluid, regardless of whether the fluid is in motion or not. It can be measured using an aneroid, a U manometer water column, or various other methods.The fundamental Bernoulli law tells the dynamic pressure in relation to air speed:
Pd = ρ*v2/2 = ρ*(U/A)2/2,
where
Pd is
the dynamic pressure
in Pa = N/m2,ρ is the density of air, ρ = 1.2 kg/m3,
v is the linear air speed in m/s, which in turn can be written as U/A, with
U being the flow rate in m3/s streaming through an area A in m2.
One application of this law is that it tells at what speed v and flow U air that will emerge from an open area A in the wall of a container holding the pressure Pd. For instance, this tells speed and consumption in the air jet that excites an organ flue pipe. These and related quantities are illustrated in the diagram of fig 2.
Another application relates to the stagnation pressure delivered by a centrifugal fan when its output is blocked, as mentioned above.
The dynamic pressure is also a primary guide to find the aerodynamic force on a body in an air stream, or with the body moving through still air. The general procedure is then that you estimate the force as the dynamic pressure times the body area. On top of that you will have to apply an empirical correction factor that applies to the specific body shape. This drag coefficient is generally not far from unity.
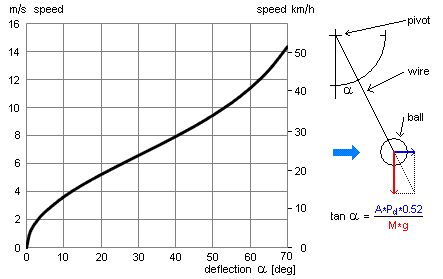 interference
with the flow, and that its measurement range should be
adequate, generally up to perhaps 10 m/s. Perhaps a bowl
cross, common with weather stations, would be too big, but
there are simple commercially available anemometers using a
small turbine, driven by the airflow. A simple low precision
device may be a hanging vane or a pendulum, a ping-pong ball
hanging from a thin wire is a classical example. Here you
can estimate horizontal air speed from the angle the
pendulum is deflected away from its vertical rest position,
fig 6.
interference
with the flow, and that its measurement range should be
adequate, generally up to perhaps 10 m/s. Perhaps a bowl
cross, common with weather stations, would be too big, but
there are simple commercially available anemometers using a
small turbine, driven by the airflow. A simple low precision
device may be a hanging vane or a pendulum, a ping-pong ball
hanging from a thin wire is a classical example. Here you
can estimate horizontal air speed from the angle the
pendulum is deflected away from its vertical rest position,
fig 6.