Q value of a pipe resonator

by Johan Liljencrants

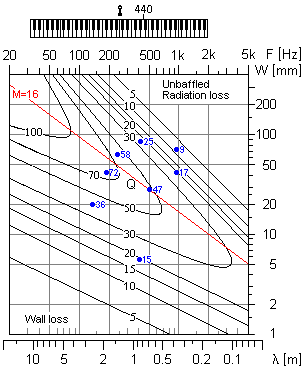
Theory

To define a resonator Q value, the archetypal way is to use the oscillating energy stored, divided by the energy lost per radian of the oscillation. There are several equivalent ways, for simplicity more common in engineering. One is to divide the resonator reactance by its series connected loss resistance, the way preferred here, or alternatively a parallel loss resistance divided by the reactance.  Elementary concepts relating to Q are outlined by Liljencrants (2002). Equivalent to Q we may use the damping factor d = 1/Q. This is motivated when the damping comes from two or more different mechanisms as in the present case of pipe resonators. We will here derive damping factors for the dominating effects, then add them into a total damping, and finally invert this sum into a resulting total Q value.

Here we basically discuss in terms of a quarter wave resonator, closed at one end, of length  , with a fundamental resonance frequency f and sound speed c.  The results are equally valid for a half wave resonator, twice as long and open both ends, such that both of the stored energy and the losses are doubled. For practical precision measurements a half wave resonator is preferred since this eliminates possible anomalies in an imperfect stopper.

The symbol  f , though without a subscript, is not used here as a general frequency variable. Instead it universally denotes the fundamental resonance frequency, thus with a firm coupling to resonator length.

Another concept, used in line theory, handles distributed losses in terms of an attenuation constant a = r/2Z + 2Z/g , where Z is the line impedance, r the series and g the shunt resistances  per unit length. Because the L - f  coupling  defines a length this can be rephrased into a damping factor  d = c a / (4 f  ).

 As a first step we settle the resonator reactance, its acoustical mass times angular frequency. With cross section area and radiusthe effective acoustical mass is

where  is the air density. The final reduction factoraccounts for the sinusoidal flow/pressure distribution within a pipe resonator, making its effective mass less than the total of the tube. Next step is to evaluate different loss mechanisms.

Radiation loss

The open end of the resonator radiates power to be heard as external sound. The energy loss because of this can be characterized by an acoustical radiation resistance. This is often told in terms of the wave number , in the baffled case and for kr<1 as (Kinsler et al (1982), p 192)

Here the rightmost rendition is obtained when the elementary relations given above are inserted. That form shows that the radiation resistance is independent of resonator area, but varies strongly with frequency. From this we derive a basic Q value, when set by radiation alone:

Considering radiation loss alone it is interesting to note that the factor A f 2 implies that different pipes with the same ratio of length to diameter will have the same Q value for the fundamental. In organ terminology such pipes are characterized by a 'halving number' to be 12. For the following calculus we  insert  the constants such that we have for the baffled case
 drad = 5.34*10-5*A f 2
and for an unbaffled pipe half as much
 drad = 2.67*10-5*A f 2
This 'free space' condition gives the minimum radiation damping attainable. Damping and radiation efficiency gradually increase as the resonator opening is put closer to a wall. The effect increases even more at the angle between two walls or in a corner, and is one of several reasons it may be difficult to measure Q in practice.

Wall loss

In the boundary layer close to the resonator wall (< 1 mm) the air is sheared as its speed goes down to zero at the wall. The effect of this viscous loss is given by Kinsler et al (1982) as an absorption coefficient, which can be reformed into an equivalent loss resistance where  is the air viscosity,  S  the circumference of the pipe, hence LS  its interior surface.  Presupposing a square pipe this can be further developed as above into a partial damping component, dominating at small areas


The viscous loss is non uniform along the pipe since it depends on local flow. Another loss mechanism comes from heat conduction into the wall, some power is lost from the temperature variations following the sound pressure, differently distributed along the pipe. Analysis already by Lord Rayleigh found that thermal damping to obey the same basic formula, only you must then augment it with a complicated multiplier to account for the gas properties. Inserting those we can use the formula for the combined viscous and heat loss once we multiply the viscosity contribution by 1.476. With the constants inserted we then find
 dwall = 1.476 dvisc = 5.71*10-3*(A f )-1/2.

Unmanageable losses

There are several additional loss mechanisms that all tend to lower the resultant Q value. One is that the wall loss may be up to a factor 2 greater than outlined above when the pipe interior surface is very ragged. Another is that the damping at the pipe open end will increase in case the acoustic particle velocity at this place is high enough that a jet is formed, indeed a normal situation with a blown organ pipe. Further the viscous loss will increase when a DC flow is superposed on the acoustic one.  All these effects are hard to predict theoretically, but they do lower the Q in a speaking pipe.

Q deteriorates when a resonator leaks near a pressure maximum, maybe through a hole or a faulty solder joint, or a crack in a wooden pipe. For an illustrative example we may recall the Rayleigh formula for the resistance of a small tube. With a leak area B and length l (wall thickness) this renders a damping  . 
For example, assuming B =1 mm2 , l =5 mm, and A =10 cm2 renders dhole = 0.178, or Q about 5. This is perhaps one tenth of what you would expect for a pipe of this area and underlines the extreme importance that pipes are faultlessly airtight. In an open flageolet pipe this effect is used to deliberately quench the fundamental resonance with a nodal hole at the middle, such that the pipe speaks at its second resonance, where the pipe length equals the wavelength.

Negligible losses

Other loss effects lend more easily to theory, but can be neglected when we regard resonators within the size range of organ pipes.  The direct radiation from the interior air into the wall material  suggests a damping like the ratio of their acoustic impedances. This ratio is to the order 2.5*10-4 from air into wood, even about 20 times smaller from air into common metals.
Absorption from viscosity and heat conduction within the air medium itself  has an attenuation constant about  f *10-6 Np/m in the audio frequency range, which transforms into the approximate damping factor  dabs = 0.00008, again completely negligible.

The issue of the resonator walls yielding to the internal pressure is an important one in speech production - the oral cavity walls have very little stiffness but are staying in place by their inertia. This results in a damping factor proportional to  f  -2 that has some influence toward low frequencies, below 1 kHz. The several loss mechanisms relevant to speech are reviewed in chapter 2 of Liljencrants (1985). Cylindrical metal or square wooden pipes are by comparison very stiff such that this effect is negligible. A known exception is the herostratic demonstration by Miller (1909) using a thin walled metal pipe with rectangular cross section. Obviously such a design has rather compliant sides and would never be used by a pipe maker.  The practical irrelevance of this effect and its consequently alleged influences from the pipe material were discussed by  Backus and Hundley (1966).

Pipe resonator Q vs. width W and fundamental resonance frequency f

Using the relations above a total Q value was computed as graphically shown in the following figures.


Fig 1.  Estimated Q vs. pipe width in an unbaffled pipe of quadratic cross section. Each curve represents a specific pipe length, either open both ends, or half as long but closed one end, resonating at the frequency indicated.

The data points are taken from Moloney & Hatten (2001), measured on 190 Hz open resonator tubes, most closely comparable to the black 200 Hz curve.
Fig 2.  Estimated Q vs. fundamental resonance frequency, each curve for a specific pipe width, baffled and quadratic cross section. Moving along the frequency axis implies a corresponding variation of resonator length.

Because of the baffling these curves are somewhat lower, compared to what is shown in figs 1 and 3.


Fig 3.  Contours of equal estimated fundamental Q in the plane of  fundamental  frequency f  vs. pipe width W, unbaffled and quadratic pipe cross section. This represents about maximum Q values attainable.

The bottom scale is for wavelength. This applies both to open pipes with a length half of this measure, and to stoppered pipes being a quarter of it.

The blue points tell results of corollary measurements, Q1 of tab 1. The red line indicates Töpfer Normalmensur.

The slope of the red line in fig 3 shows how width varies with frequency in a pipe rank with halving number M=16. The vertical position of this line is put similar to the Töpfer Normalmensur with W =137 mm at 8'C (65 Hz), same area as for diameter 155 mm.  One may speculate whether pipe makers of the past have lead the evolution of pipe scaling toward maximum Q.

Corollary measurements were made on a few cylindrical tubes and household items, dimensions given in tab 1. For fig 3 their diameters were recomputed into W giving same cross sectional areas, .  The results conform reasonably well with the theory.

Mtrl
Type Dia (mm)
 Len (mm)
 f  (Hz)
 Q1 Q2 Q3 Q4 Q5
Tab 1. Measured data for the sample resonators, Q  for the resonances at up to 5 times f. The fundamental Q1 are indicated in blue in  fig 3.

The abnormally high Q3 in parentheses is probably due to a cross resonance in this very wide cavity.










glass closed 93 177 418 25 ---
 14 ---
porcel closed 78 66 957 9
 ---
 (28) ---
PVC open 69 667 243 58 69 45
22
PVC open 46 872 188 72 92 77 67 60
PVC open 46 148 959 17 33 27

cardb open 31 308 511 47 54 45
30
PVC open 22 1234 135 36 48 62
78
PVC closed 6
 205 409 15 ---
 30 ---


Q of higher resonances

The diagrams here apply to the fundamental resonance only, but we can grossly estimate Q for the higher resonances at  frequencies n f,  n =2, 3, 4, ... for open pipes, n =3, 5, 7, ... for pipes closed one end.

With wide pipes where the radiation loss dominates, then the pipe reactance goes in proportion to n while the radiation resistance increases as n2.  For the higher resonances Q is then estimated to fall off as 1/n .

With narrow pipes where the wall losses dominate, then the pipe reactance still goes in proportion to n while the loss resistance increases only as n1/2.  Q is then estimated to rise of as n1/2 initially, until the radiation loss takes over to impose its n-1 dependency, which happens at a higher frequency than the break over for the fundamental. This should be a valid explanation to why narrow violin type pipes have relatively prominent higher harmonics.

Practical Q measurement

To measure Q of a resonator pipe an obvious way is to place a microphone inside it and irradiate the ambient space with an exciting sound. Then examine the microphone sound level while frequency is swept over the applicable range. However, it is not trivial to keep the exciting sound field under control. The loudspeaker has a frequency response that can deviate considerably from ideally flat, with resonances that may interfere with those of the pipe under test. And if the experiment is done indoor the room will add innumerable other resonances to the ambient field. 

Measuring higher resonances pose the additional problem that the internal microphone should be placed near a pressure maximum for the resonance in question. For instance, in an open pipe the optimal microphone position  for the fundamental resonance is at the middle of the pipe. But that point is a node for the second resonance, so this one can hardly be measured unless the microphone is moved.

The corollary  measurements of tab. 1 used the program 'TombStone' by S Granqvist, nicknamed after a classical Brüel & Kjaer electromechanical generator and level recorder. This program can record sound levels from two microphones. One was placed inside the resonator and one outside for reference, near the speaker. Then the resonance curve was taken as the difference between them, such that the loudspeaker response was compensated for. To avoid room interference the measurements were made outdoors, over a sound absorbing foam mattress. Also tracking bandpass filtering was done on the microphone signals to reduce ambient noise.


Fig 4. Frequency sweep recording example, showing disturbance from a room. Blue is from the resonator internal microphone, red external reference, and black difference between them.  Green figures tell the five lowest resonances. The second resonance peak is rather low because the microphone was located near the middle of the open specimen pipe. A and B denote spurious peaks due to reflections from the floor.
Despite such precautions one has to watch the reference record to be reasonably smooth near the pipe resonance to be measured. A particularly dangerous situation is when a nearby reflecting surface (e.g. the table) allows a dual sound path from speaker to reference microphone.  Then total cancellation may come at some frequencies, such that the difference record shows narrow peaks, falsely suggesting resonances with Q values that are high beyond all reason.

A different way to determine Q is from the time response of the resonator when excited by an impulse. This method may be easier to use when Q is moderately low, such that the peaks in a frequency response are less prominent. The response is taken from a microphone inside the resonator, and the impulse may be generated by discharging a capacitor through an external tweeter loudpeaker. An impulse of even better quality (better flatness in frequency spectrum) comes from an electric spark, perhaps generated using a car ignition coil. Another merit with this is that the spark gap can easily be placed inside the resonator, such that signal level is increased and ambient room acoustics problems are minimized.


Fig 5. Decay after a driving sinusoid near resonance is turned off. Left with the resonator in semi free space, right resting on the floor such that its open end is baffled. The difference between the cases is possibly exaggerated since some room reverberation interferes. Left it amplifies, right it comes in counter phase to the resonator oscillation.

A more refined alternative is to feed with a sinusoidal signal at a frequency close to the resonance, such that only one resonance is excited. Then study the resonator decay immediately after the excitation is abruptly turned off. We can now compute  where a is the ratio between the first and second peak-to-peak values measured, and n is the number of periods between them, see further Liljencrants (2002).  Still one must watch out for  possible disturbances from the ambience.  There may linger reverberant sound in the room, corrupting the low level late portion of the recording.


Conclusions

The loss mechanisms in a pipe resonator were reviewed. The dominating loss with wide pipes is the radiation to the environment, while viscous shear and heat transfer into the pipe wall dominates with narrow pipes. Theoretical results are shown in fig 3 as contours of equal Q in the plane of frequency vs. pipe width. This diagram is equally applicable to open half wavelength pipes as to open-closed quarter wavelength pipes. The theoretical predictions are reasonably verified by a few practical measurements. It is interesting to note that classical Töpfer pipe scaling closely follows a trajectory of maximum Q.

References

  • Backus J, Hundley T C (1966): Wall Vibrations in Flue Organ Pipes and Their Effect on Tone.  J. Acoust. Soc. Am. 39 (5), pp 936-945.
  • Beranek L L (1957): Acoustics. McGraw-Hill.
  • Granqvist S: TombStone level recorder program for Windows ®.
  • Kinsler L E, Frey A R, Coppens A B, Sanders J V (1982): Fundamentals of acoustics.  3rd ed. John Wiley & Sons.
  • Liljencrants J (1985): Speech Synthesis with a Reflection-type Line Analog. Diss., Roy. Inst. Tech., Stockholm. http://www.fonema.se/thesis/JLreflex.pdf  (6.5MB)
  • Liljencrants J (2002): Resonators and Q value. http://www.fonema.se/qval/qval.htm   http://www.mmdigest.com/Tech/qval.html
  • Miller D C (1909). Science 29, pp 161-171.
  • Moloney M J, Hatten D L (2001): Acoustic quality factor and energy losses in cylindrical pipes. Am. J. Phys. 69 (3), pp 311-314. Summary at http://www.rose-hulman.edu/~moloney/AcousticWork/QualityFactorsofCylindricalPipes.html
  • Lord Rayleigh: Theory of sound. 2nd ed 1929, Macmillan & Co Ltd.
    		•

    2006-10-19